Fast & Slow Pointers Note

The typical algorithm using fast and slow pointers is LeetCode 141.

Given head, the head of a linked list, determine if the linked list has a cycle in it.

Define two pointers start from head with different speed, the fast pointer move 2 steps each time while the slow pointer move 1 step each time. If there’s no cycle in the LinkedList, the fast pointer will reach a null, then return. If there is a cycle, the faster and slow pointer will finally meet.

Why we define fast speed to 2 steps and slow to 1 step

They must meet in the cycle

When slow pointer reaches the cycle, the faster should be already in the cycle, and the fast is chasing the slow. Say the fast is one or two steps away from the slow:

• If they are one step away, they’ll meet on the next movement.
• If they are two steps away, they’ll meet on the next next movement.

Easy to find cycle starting point

Let k be the steps when pointers meet, then the fast has run 2k steps, k steps more than the slow.

This is illustrated by the following picture.

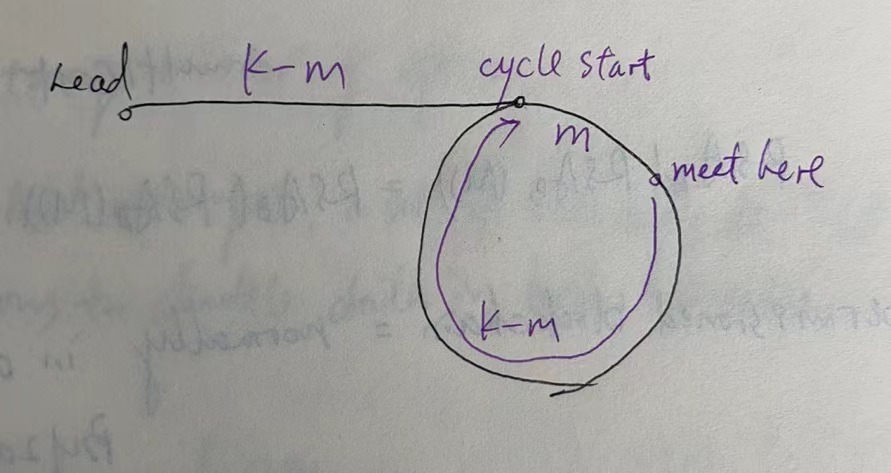
Move the slow pointers back to the head, after k - m steps, the two pointers will meet at the start point of the cycle.

Simple and efficient

Let

• fast = k * slow
• w is the distance from head to cycle start
• s is perimeter of the cycle
• j is the movement where j > w and j mod s = 0
• fast and slow meet at X[j]

We have the fast ran kj - j = (k-1)j steps more than the slow. Since j mod s = 0, the fast meets the slow at the position X[j], so the two pointers will always meet at some point on the cycle. And we know that, if k is greater, the fast pointer will run more rounds before two pointers meet, so the factor 2 is the best.